O objetivo desta unidade é desenvolver o raciocínio lógico por meio de noções básicas da lógica matemática, com atividades envolvendo proposições simples e compostas, identificando os seus valores lógicos e construindo a ideia de como avaliar os argumentos pela construção da tabela verdade.
Proposições e conectivos
Verdade e Coerência
Muitas frases que utilizamos, no dia a dia, podem ser classificadas em VERDADEIRAS ou FALSAS. Por exemplo, são verdadeiras as frases:
- “Paris é capital da França.”
- “Dois mais dois é igual a quatro.”
- “Um dia tem 24 horas.”
Enquanto que são falsas as frases: - “Buenos Aires é capital do Brasil.”
- “Dois mais dois é igual a cinco.”
- “Uma semana tem 10 dias.”
Existem , no entanto, frases que não podem ser classificadas assim, como, por exemplo:
-“Que horas são?” - “Não faça isso!”
Uma frase que pode ser classificada com Verdadeira ou falsa, não podendo ser as duas coisas simultaneamente, é chamada de PROPOSIÇÃO.
Cálculo proposicional é uma parte da lógica matemática a qual se estuda a validade de argumentos por meio de uma linguagem própria, a linguagem proposicional.
Proposição é toda sentença declarativa que pode ser classificada, unicamente, como verdadeira (V) ou falsa (F). Chama-se valor lógico de uma proposição a verdade se a proposição for verdadeira e a falsidade de se proposição for falsa.
As proposições são designadas por letras latinas minúsculas.
Exemplo 1:
p: Pedro é estudante
q: Ana é bailarina
Proposição Composta é formulada pela combinação de duas ou mais proposições.
Cada uma das expressões usadas para unir tais proposições ou transformar uma proposição formando uma nova proposição, é chamada de conectivos lógicos.
Exemplo 2:
p: Pedro é estudante e Ana é bailarina.
q: Pedro é estudante ou Ana é bailarina.
r: Ou Pedro é estudante ou Ana é bailarina.
s: Se Pedro é estudante, então Ana é bailarina.
t: Pedro é estudante se, e somente se Ana é bailarina.
Os conectivos grifados podem ser representados por:
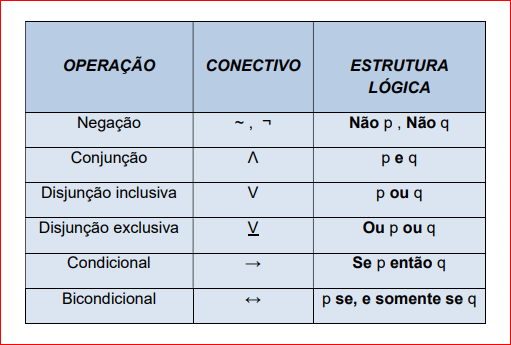
Dessa forma, se p: Pedro é estudante e q: Ana é bailarina, poderíamos também escrever tais proposições compostas da forma:
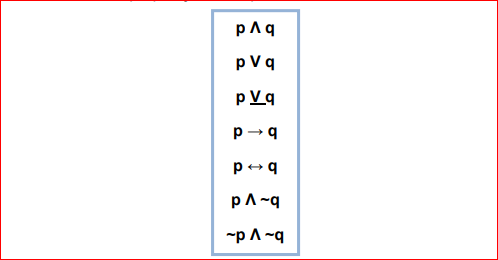
Outra maneira de efetuar a negação é antepor à proposição expressões como “não é verdade que”, “é falso que”.
Exemplo 3:
A negação de p: Pedro é estudante é:
- ~p: É falso que Pedro é estudante.
- ~p: Não é verdade que Pedro é estudante.
- ~(~p): Não é verdade que Pedro não é estudante – equivale a Pedro é estudante.
Então a negação da negação de p afirma o mesmo que p.
Exercícios propostos
- Dê o valor lógico verdadeiro (V) ou falso (F), nas sentenças que são proposições abaixo, e marque um X quando não for possível:
a) Salvador é a capital da Bahia ( V)
b) -5 pertence ao conjunto Z ( V)
c) Que raiva! ( X)
d) Todos os animais são mamíferos ( F)
e) Quero tirar férias! ( X)
f) Mercúrio não é um planeta do sistema solar. (F )
g) Pitágoras era um grande matemático. ( V)
h) Henrique é físico. ( X)
i) Ela é uma boa professora. (X )
j) Gostaria de uma xícara de chá. (X )
k) Qual é o seu nome?. ( X)
l) As nuvens são feitas de algodão. (F ) - Transforme as proposições simples em proposições compostas:
a) p: Ana estuda matemática
q: Caio estuda história
p Ʌ q: Ana estuda matemática e Caio estuda história
b) p: Faz frio
q: Faz calor
p V q: Faz frio ou faz calor
c) p: Bia estudou veterinária
q: Bia gosta de animais
p → q: Se bia estudou veterinária, então Bia gosta de animais.
d) p: x pertence ao conjunto dos números naturais
q: x é um número inteiro e positivo
p ↔ q: x pertence ao conjunto dos números naturais se, e somente se x é um número inteiro e positivo
e) p: Gosto de sorvete
q: Gosto de refrigerante
p Ʌ ~q: Gosto de sorvete e não gosto de refrigerante
f) p: Vou ao restaurante
q: Vou ao cinema
p V q: Vou ao restaurante ou vou ao cinema
- Sejam as proposições p: Paulo é feliz e q: Paulo é atleta. Traduzir para a linguagem simbólica as seguintes proposições:
a) Paulo é feliz e atleta: p Ʌ q
b) Paulo é feliz e não é atleta: p Ʌ ~q
c) Se Paulo é feliz então Paulo é atleta: p → q
d) Não é verdade que Paulo é triste ou atleta : p V q
e) Paulo não é feliz e não é atleta:
f) Paulo é atleta se, e somente se é feliz:
g) Paulo é feliz ou é triste e atleta:
h) É falso que Paulo e feliz ou que não é atleta:

